As the complexity of a physical system increases, the training of a metamodel by artificial neural network becomes more challenging. In this scenario, creating a suitable training dataset may become laborious and expensive, thus, one often has to make a compromise between cost and accuracy. Transfer learning (TL) is a common approach that can be employed to mitigate this issue by using knowledge from a source domain to improve the learning of a target domain with limited data. One approach to TL is to use a multi-fidelity training procedure to improve model accuracy by applying higher-fidelity training data to a model trained on low-fidelity data. This method was shown to effectively reduce training costs in previous studies.
One can conceive of several case examples for the application of TL in heat transfer systems: The need for TL may arise when the performance of a heat exchanger is affected due to fouling over time, or TL can be applied to construct a semi-empirical metamodel using readily available simulation data and limited experimental data. TL can also enable us to use information from a low-cost two-dimensional metamodel to account for three-dimensional effects using a small three-dimensional dataset. Moreover, TL is especially beneficial for domain adaptation, where information from a different (but related) heat transfer system can be applied to solve problems in another system (e.g., heat transfer from vertical and horizontal walls can be related to heat transfer from an enclosure).
The key parameter characterizing a natural convection problem is the Rayleigh number (Ra). This parameter is defined as the product of the Grashof number (the ratio of buoyancy to viscous forces), and Prandtl number (Pr, the ratio of momentum and thermal diffusivity). However, various expected and unexpected factors can affect a natural convection system (i.e., some features may become active under different conditions, or after a system is redesigned). For example, the system’s orientation with respect to gravity or the system’s boundary conditions may change, or applying a magnetic force to the system could lead to thermomagnetic or magnetohydrodynamic effects. Moreover, generating a new set of simulations or experiments can be a laborious process. Domain adaptation or TL with deep neural networks (DNN) can be employed to remedy these problems.
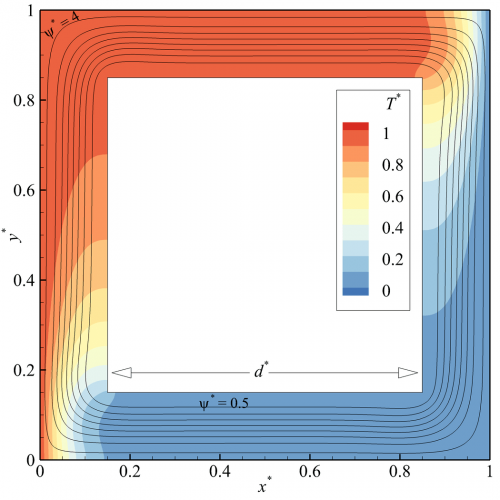
We considered hollow enclosures with their inner walls being adiabatic while the other boundary conditions were the same as the original benchmark problem. The details of the numerical method and its verification can be found in [1]. To account for the grid size dependency, we compared the results of the average Nu as well as the maximum stream function for different grid sizes. The dimensionless temperature and stream function results for a simulation conducted for an air-filled hollow enclosure are presented in Fig. 1.
We aimed to extract a metamodel out of a physical model that numerically predicts the natural convection characteristics of hollow enclosures filled with Newtonian fluid. Other than the hollow width (d*), this problem is governed by two other parameters: Ra and Pr (see here for details). We consider Ra of up to 108 and Pr of greater than 0.05; however, lower Pr were also considered provided that the ratio of Ra/Pr is less than 108.
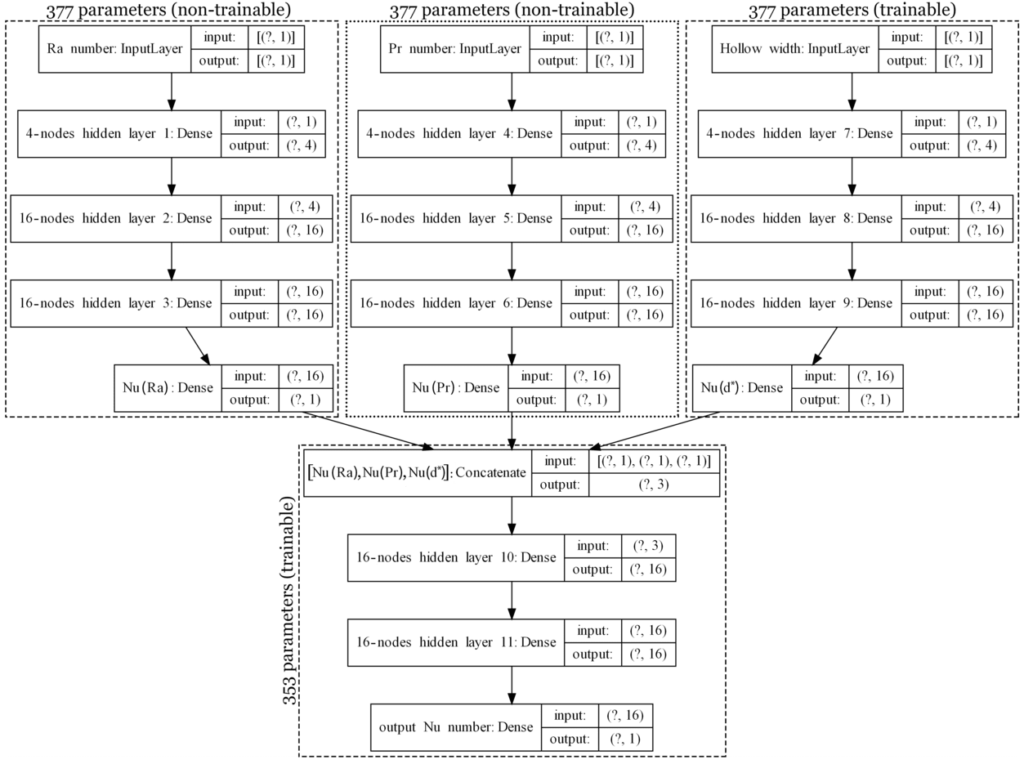
We employed the already trained DNN from the benchmark problem (presented here) and transferred its learning to this new problem. The structure of the new DNN along with its training details are shown in Fig. 2. This structure is created by adding a new branch to account for variations of d* before combining all branches. Therefore, we froze the training on the two former branches (given that they were already trained), and only trained the new branch and the last two hidden layers (located after the concatenate layer, Fig. 2).
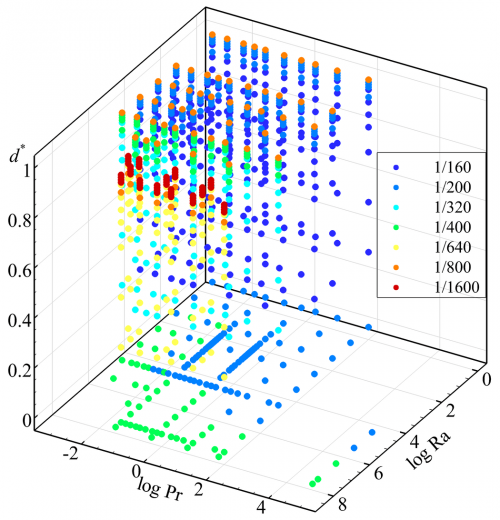
We generated a dataset of 798 simulations for different inner widths (d*= 0.3, 0.5, 0.7, 0.8, 0.85, 0.9, 0.92, 0.95, 0.96, 0.97, 0.98, and 0.99) and combined it with the training data outlined in the original problem for d*=0. The case of d*=0 describes the enclosures no hole at the center and the case of d*=1 refers to a trivial case with no heat transfer domain (i.e., Nu=0). To generate our training dataset, we used a multi-grid approach (described here) based on the values of Ra and d*. The dimensionless grid sizes for d* ranging from 0.3 to 0.9 were 1⁄160, 1⁄320, and 1⁄640 for Ra≤104, 104<Ra<107, and Ra≥107, respectively. However, for larger inner widths, our model required finer grid sizes as small as 1⁄1600. The scatter graph for the training dataset is presented in Fig. 3.
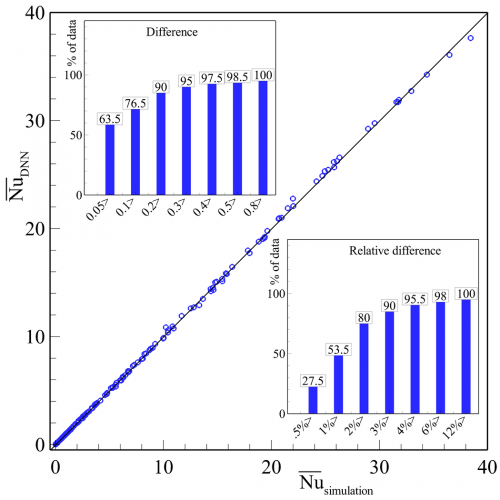
The training error for more than 20% of our data points was above 1%, which was higher than the maximum error resulting from an insufficient grid size. A further improvement in metamodel accuracy can be achieved by adding more data points wherever the training error is relatively high. The test result for our Nu metamodel for hollow enclosures is summarized in Table 1. For comparison, we also included the test result for an optimized model that did not benefit from TL, demonstrating that our TL approach resulted in an improved mean squared error of 63%. A scatter graph of predicted Nu values using the DNN metamodel versus our simulation data is presented in Fig. 4. The average and maximum differences between the predicted and simulated Nu results for the TL metamodel are 0.075 and 0.803, respectively. This test was carried out using a dataset of 200 simulations using the highest fidelity grid systems for d*= 0, 0.2, 0.4, 0.6, 0.78, 0.82, 0.88, 0.91, 0.94, 0.965, and 0.985.
|
|
MSE (/10-5) |
MAE (/10-3) |
MRE (%) |
SD (%) |
|
TL approach |
7.18 |
5.82 |
1.34 |
1.44 |
|
Without TL |
19.46 |
8.08 |
1.86 |
2.59 |
In comparison with the original enclosure, hollow enclosures do not necessarily have lower heat transfer performance. Even though the heat transfer domain is smaller, a narrow passage brings higher velocity gradients, and therefore, this combined effect may produce higher overall Nu. Thus, at fixed Ra and Pr, there exists a non-zero inner width (d*) for maximum Nu. For example, for air-filled enclosures, a d*=0 enclosure has the highest Nu at Ra=103. However, as Ra increases, the maximum Nu is seen at larger d* (e.g., d*≅0.5 for Ra=105, and d*≅0.85 for Ra=108). Our Nu metamodel can be exploited to provide these optimum inner widths for all Ra and Pr.
We conclude that our metamodel can be retrained to predict Nu for different natural convection problems. This TL strategy is versatile and can handle straightforward metamodeling problems for many different engineering systems.