While a composite piezoresistive pressure sensor can only be composed of a sensing layer integrated with a pair of signal detection electrodes, finding efficient polymer-filler compositions and their manufacturing processes for specific applications is complicated and costly. Numerical and experimental methods are used to understand and predict the underlying mechanisms for different polymer matrices and additive fillers. Development of sensing elements through special nano- and micro-structures offers strategies for enhancing stretchability, sensing performance, and durability. Design modifications by microstructuring the electrodes are also recommended to improve the performance of piezoresistive strain/pressure sensors.
Using in-plane (single-sided) interdigitated electrodes is beneficial in terms of the fabrication process (one less layer and ease of integration on a printed circuit board (PCB)). While covering a broader pressure range, in-plane interdigitated electrodes suffer from low sensitivity. Moreover, the equivalent resistance for sensors with interdigitated electrodes cannot be straightforwardly estimated, unlike polymeric sensors with parallel plate electrodes or MEMS-based piezoresistive sensors. Other than limited experiments [1,2], no systematic design procedure for in-plane electrodes in composite polymer sensors is available.
We build a neural network metamodel for the resistance response using the numerical model presented in the previous post. We use the metamodel to predict the sensor performance for various electrode arrangements and find the optimal one through a multi-objective optimization targeting the maximum sensitivity and minimum power consumption.
To show the effect of electrode configuration on the sensor performance, we tested all possible cases on PCBs divided into nine equal-sized squares as presented in Fig. 1. There were eight applicable cases under the constraints of (1) fixing the electrode connections at two points located at one side of the PCB, (2) disregarding the discontinuous electrodes (to avoid multiple electrode connections), and (3) removing the cases mirrored with respect to electrode connections (identical results). As illustrated in Fig. 1, the sensor performance is highly dependent on the electrode design. As we see from the resistance–pressure characteristics, the curves are not monotonic, and therefore, the comparison made for 100 kPa is not valid for other pressures. The non-monotonic response also does not allow us to use these wide electrodes for measurement (because of not providing unique measurements).
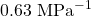 ) at 100 kPa; however, this is not valid for the whole range, as can be seen from the characteristics shown on the right side. Other than the low sensitivity (compare with the N3 electrode, which exhibits a sensitivity of
) at 100 kPa; however, this is not valid for the whole range, as can be seen from the characteristics shown on the right side. Other than the low sensitivity (compare with the N3 electrode, which exhibits a sensitivity of  at 100 kPa), the curves are not monotonic, and therefore, one cannot use these wide electrodes.
at 100 kPa), the curves are not monotonic, and therefore, one cannot use these wide electrodes.Similarly, we examined the sensor performance for different electrode configurations on the 4![]() 4 resolution PCB matrix as presented in Fig. 2. If we divide the PCB plate into n
4 resolution PCB matrix as presented in Fig. 2. If we divide the PCB plate into n![]() n square regions, there are
n square regions, there are ![]() possible electrode configurations. Nonetheless, the 4
possible electrode configurations. Nonetheless, the 4![]() 4 PCB only takes 445 applicable cases out of
4 PCB only takes 445 applicable cases out of ![]() under the constraints we set. The sensor performance for all the applicable cases is summarized in the video presented below the figure. The electrode labeled as the best configuration in Fig. 2 resulted in the highest sensitivity for both 50 and 100 kPa pressures (for 10 kPa, this configuration exhibited 3.5% less sensitivity than the highest achieved sensitivity). However, we note that there were other electrodes with non-monotonic characteristics, which resulted in better sensitivities for lower pressures.
under the constraints we set. The sensor performance for all the applicable cases is summarized in the video presented below the figure. The electrode labeled as the best configuration in Fig. 2 resulted in the highest sensitivity for both 50 and 100 kPa pressures (for 10 kPa, this configuration exhibited 3.5% less sensitivity than the highest achieved sensitivity). However, we note that there were other electrodes with non-monotonic characteristics, which resulted in better sensitivities for lower pressures.

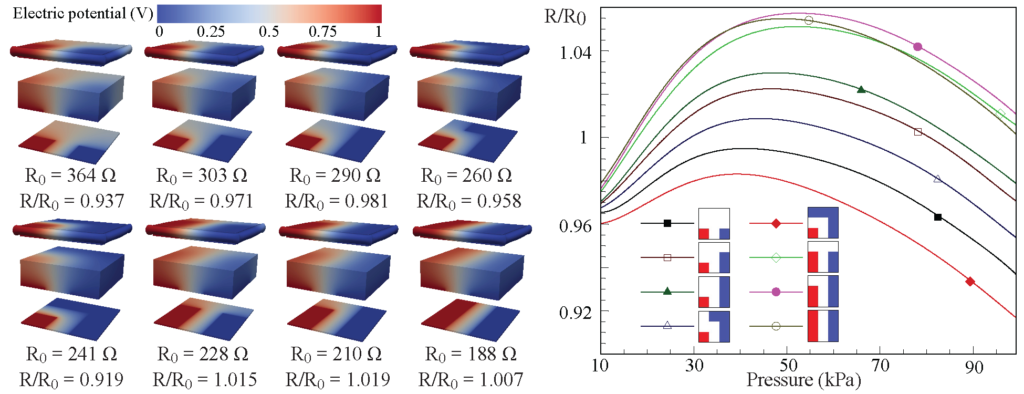
 4 resolution PCB matrices. (a) and (b) The histogram graphs for the results of sensitivity and resistance ratio, respectively. We listed the best and worst cases in (c) and (d), respectively (for 100 kPa). (e) The electric potential and electric field distributions for the best and worst configurations for the sensor at rest. For the worst case, a uniform current density inside the sensing layer leads to poor performance. (f) The resistance–pressure and sensitivity–pressure characteristics for the best and worst configurations.
4 resolution PCB matrices. (a) and (b) The histogram graphs for the results of sensitivity and resistance ratio, respectively. We listed the best and worst cases in (c) and (d), respectively (for 100 kPa). (e) The electric potential and electric field distributions for the best and worst configurations for the sensor at rest. For the worst case, a uniform current density inside the sensing layer leads to poor performance. (f) The resistance–pressure and sensitivity–pressure characteristics for the best and worst configurations.Further improvement in the sensitivity could be expected by increasing the PCB design resolution. There are numerous applicable cases for higher PCB resolutions, and a direct comparison is not feasible. Nonetheless, we built artificial neural network (ANN) models to predict the sensor performance for different electrode configurations on the 5![]() 5 PCB. We have trained the ANNs using the Keras 2.4.3 library with TensorFlow 2.4.1 [3] as the backend. We used Adam optimizer [4] for backpropagation and optimized the neural networks using the approach presented in [5]. The details of the neural network architecture for the metamodeling are available here. We employed a multi-fidelity strategy [6] to reduce the training cost. To generate our low-fidelity data, we decreased the grid size for electrostatic simulation from 128
5 PCB. We have trained the ANNs using the Keras 2.4.3 library with TensorFlow 2.4.1 [3] as the backend. We used Adam optimizer [4] for backpropagation and optimized the neural networks using the approach presented in [5]. The details of the neural network architecture for the metamodeling are available here. We employed a multi-fidelity strategy [6] to reduce the training cost. To generate our low-fidelity data, we decreased the grid size for electrostatic simulation from 128![]() 120
120![]() 120 to 64
120 to 64![]() 60
60![]() 60. Because the effect of the PCB configuration on the mechanical deformation is negligible (thin layer), we used a single simulation result for the displacement distribution for all the electrodes and skipped the mechanical problem. By also decreasing the tolerance of the Newton solver, we sped up the simulation by 81%. We defined a cost function (CF) as the product of the total simulation time and the mean squared error of the predictions on a test dataset (2,000 high-fidelity simulations). We compared the results of the CF to see if using more low- or high-fidelity data efficiently improves the model accuracy. As presented in Fig. 3, we trained our ANN model using 500 high-fidelity data as the first step. Comparing steps 2a (pretraining the model using low-fidelity data) and 2b (adding more high-fidelity data) showed that using 2000 low-fidelity data improved the model accuracy at a lower CF than increasing the size of the high-fidelity dataset to 1000. Therefore, we increased the size of the low-fidelity dataset in the third and fourth steps. Because of the increase in the CF at step 4, we switched to the high-fidelity data and added 1000 more data to finally achieve a prediction error of
60. Because the effect of the PCB configuration on the mechanical deformation is negligible (thin layer), we used a single simulation result for the displacement distribution for all the electrodes and skipped the mechanical problem. By also decreasing the tolerance of the Newton solver, we sped up the simulation by 81%. We defined a cost function (CF) as the product of the total simulation time and the mean squared error of the predictions on a test dataset (2,000 high-fidelity simulations). We compared the results of the CF to see if using more low- or high-fidelity data efficiently improves the model accuracy. As presented in Fig. 3, we trained our ANN model using 500 high-fidelity data as the first step. Comparing steps 2a (pretraining the model using low-fidelity data) and 2b (adding more high-fidelity data) showed that using 2000 low-fidelity data improved the model accuracy at a lower CF than increasing the size of the high-fidelity dataset to 1000. Therefore, we increased the size of the low-fidelity dataset in the third and fourth steps. Because of the increase in the CF at step 4, we switched to the high-fidelity data and added 1000 more data to finally achieve a prediction error of ![]() (mean
(mean ![]() standard deviation of the relative errors). In all cases, we augmented the training data by flipping horizontally (identical simulation results). Similarly, we built another model for predicting the initial resistance based on the electrode shape (with a test error of
standard deviation of the relative errors). In all cases, we augmented the training data by flipping horizontally (identical simulation results). Similarly, we built another model for predicting the initial resistance based on the electrode shape (with a test error of ![]() ).
).
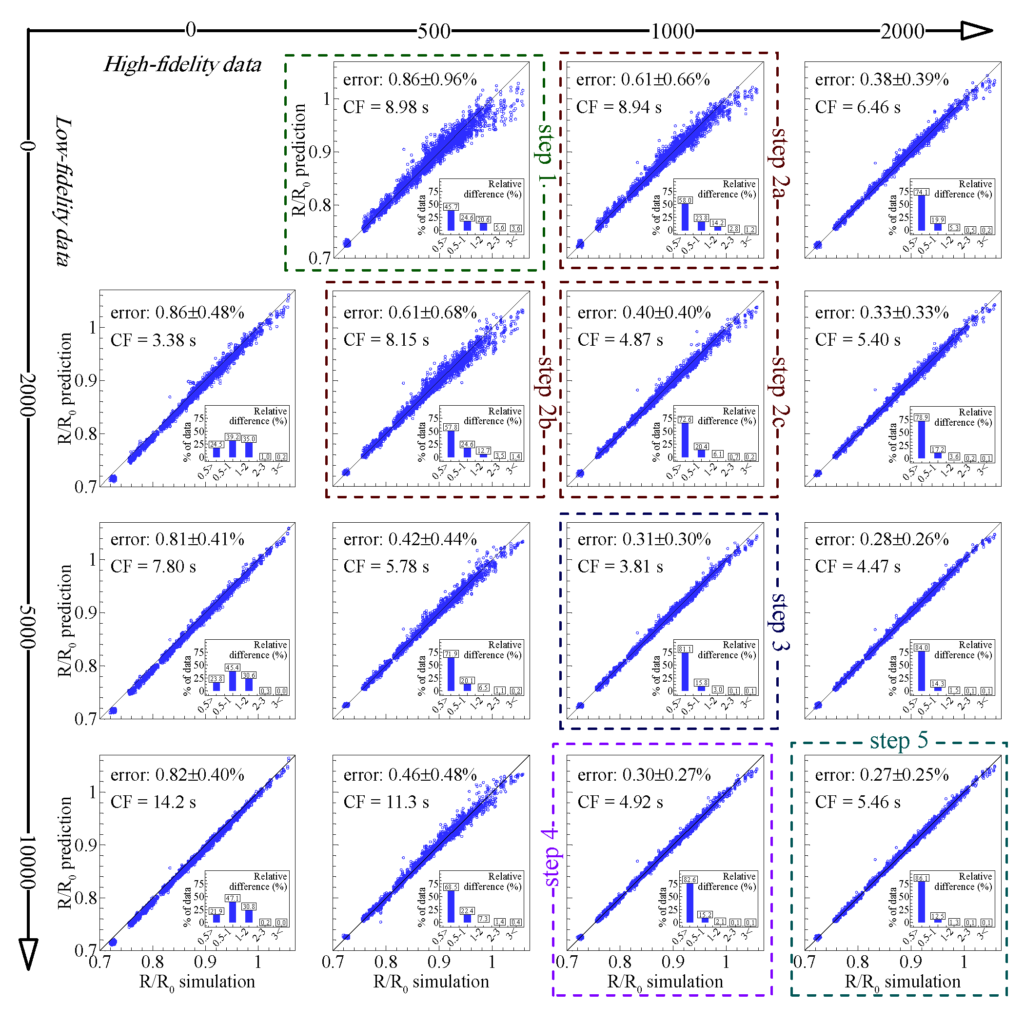
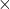 5 resolution PCB. The prediction errors associated with the metamodels built using different sizes of low- and high-fidelity datasets are presented.
5 resolution PCB. The prediction errors associated with the metamodels built using different sizes of low- and high-fidelity datasets are presented.We applied the constructed ROMs on 49,305 electrode configurations (all applicable cases out of 49,305 possible combinations) and found the cases with the highest sensitivities, highest initial resistance, and lowest initial resistance (Fig. 4a). We ran FEM simulations for every 50 top cases to be assured of the results generated by our ROMs.
Other than the sensor sensitivity, the value of the initial equivalent resistance is of particular interest to minimize power consumption and reduce heat dissipation. The electric power is given by ![]() for the sensor powered by a constant current source and by
for the sensor powered by a constant current source and by ![]() for the case of a constant voltage source. Therefore, the second objective is to minimize the initial resistance if the sensor is driven by a constant current source (or to maximize it for a constant voltage source). To combine the two objectives, we defined normalized sensitivity and initial resistance as
for the case of a constant voltage source. Therefore, the second objective is to minimize the initial resistance if the sensor is driven by a constant current source (or to maximize it for a constant voltage source). To combine the two objectives, we defined normalized sensitivity and initial resistance as
![]() (1)
(1)
where the minimum and maximum values are known through the ANN model. Using the weighted metric method, we aimed to minimize
![]() (2a)
(2a)
for a constant current source, or
![]() (2b)
(2b)
for a constant voltage source. In Eq. (2), ![]() is a distance metric, and w
is a distance metric, and w![]() and w
and w![]() are the weights of the objectives chosen based on the relative importance of the sensor sensitivity or electric power consumption. Using the results of the ANN predictions for the 49,305 electrode configurations, we found the multi-objective optimal case as shown in Fig. 4b through Eq. (2a) for equal weights (for any p higher than 2).
are the weights of the objectives chosen based on the relative importance of the sensor sensitivity or electric power consumption. Using the results of the ANN predictions for the 49,305 electrode configurations, we found the multi-objective optimal case as shown in Fig. 4b through Eq. (2a) for equal weights (for any p higher than 2).

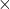 5 resolution PCBs. (a) The cases with the highest sensitivity and highest and lowest initial resistance. (b) The optimal cases giving the best trade-off between maximizing sensitivity and minimizing power consumption.
5 resolution PCBs. (a) The cases with the highest sensitivity and highest and lowest initial resistance. (b) The optimal cases giving the best trade-off between maximizing sensitivity and minimizing power consumption.We note that the contact resistances between the electrodes and the sensing layer affect the sensor performance. The contact resistance can be effectively independent of the applied pressure [36]; however, it may be affected by other factors such as material properties, contact area, surface roughness, oxide formation, contamination, and other environmental conditions. Here, we neglected the resistivity of the electrode material, and considered a contact resistance in the form of
![]() (3)
(3)
where A1 and A2 are the total surface area of the electrodes in contact with the sensing layer, and ![]() is a constant. The electrical resistivity of the sensing layer
is a constant. The electrical resistivity of the sensing layer ![]() is 0.96 and 0.53
is 0.96 and 0.53 ![]() .m for the composite at rest and 100 kPa loading, respectively. Using Eq. (3), an electrode on the 5
.m for the composite at rest and 100 kPa loading, respectively. Using Eq. (3), an electrode on the 5![]() 5 PCB may have a contact resistance in the range of 0.48 to 4.8 Ω (0.26 to 2.6 Ω at 100 kPa). In Fig. 4b, the optimal cases are also listed considering the effect of contact resistance on the sensor characteristics. As we see, because the 5
5 PCB may have a contact resistance in the range of 0.48 to 4.8 Ω (0.26 to 2.6 Ω at 100 kPa). In Fig. 4b, the optimal cases are also listed considering the effect of contact resistance on the sensor characteristics. As we see, because the 5![]() 5 PCBs have high resistances, the contact resistance had little effect on the results. However, for higher resolution PCBs with lower average distance between the electrodes, the effect of contact resistance should be considered.
5 PCBs have high resistances, the contact resistance had little effect on the results. However, for higher resolution PCBs with lower average distance between the electrodes, the effect of contact resistance should be considered.
Using a multi-fidelity approach, we trained convolutional neural networks (CNNs) to predict the equivalent resistance (initial value and the change) for different electrode arrangements on the 10![]() 10 PCBs. The details of the deep learning model are presented here. We conducted a total of 140,000 high-fidelity simulations with four different locations for the electrode connections (Fig. 5a) at 100 kPa (a strain of about 66.5%). The high electrical conductivity of the electrode material enabled us to combine the high-fidelity simulations for all the electrode connections and augment the data by rotating (90, 180, and 270 degrees) and flipping as well. To generate a low-fidelity dataset, we used the predictions from the ANN model for the 49,305 electrode configurations on the 5
10 PCBs. The details of the deep learning model are presented here. We conducted a total of 140,000 high-fidelity simulations with four different locations for the electrode connections (Fig. 5a) at 100 kPa (a strain of about 66.5%). The high electrical conductivity of the electrode material enabled us to combine the high-fidelity simulations for all the electrode connections and augment the data by rotating (90, 180, and 270 degrees) and flipping as well. To generate a low-fidelity dataset, we used the predictions from the ANN model for the 49,305 electrode configurations on the 5![]() 5 PCBs and increased their resolution to 10
5 PCBs and increased their resolution to 10![]() 10. We pre-trained the CNNs using a dataset including 40,000 high-fidelity simulations combined with 49,305 low-fidelity data (split into 85,000 training data and 15,000 validation data). Subsequently, we trained the CNNs using 125,000 high-fidelity simulations (total of 1 million data after augmentation) and tested the models for the sensitivity and initial resistance using 30,000 test data (generated by 15,000 high-fidelity simulations) as shown in Fig. 5b. We evaluated the sensitivity and initial resistance for 315 million different configurations using our trained CNNs (runtime of 4.5 hours using 8
10. We pre-trained the CNNs using a dataset including 40,000 high-fidelity simulations combined with 49,305 low-fidelity data (split into 85,000 training data and 15,000 validation data). Subsequently, we trained the CNNs using 125,000 high-fidelity simulations (total of 1 million data after augmentation) and tested the models for the sensitivity and initial resistance using 30,000 test data (generated by 15,000 high-fidelity simulations) as shown in Fig. 5b. We evaluated the sensitivity and initial resistance for 315 million different configurations using our trained CNNs (runtime of 4.5 hours using 8![]() 128GB of memory and 8
128GB of memory and 8![]() 28 CPUs via two 2.4 GHz E5-2680v4 Intel Xeon processors). We normalized the results of the predictions using Eq. (1) and employed Eq. (2) to find the optimal cases (for
28 CPUs via two 2.4 GHz E5-2680v4 Intel Xeon processors). We normalized the results of the predictions using Eq. (1) and employed Eq. (2) to find the optimal cases (for ![]() and equal objective weights). We found the ones presented in Fig. 5c to exhibit a high sensitivity with low operating power. We compared the predicted results for the best cases (the 400 top results) with the FEM simulations and found good prediction accuracies (errors of
and equal objective weights). We found the ones presented in Fig. 5c to exhibit a high sensitivity with low operating power. We compared the predicted results for the best cases (the 400 top results) with the FEM simulations and found good prediction accuracies (errors of ![]() for
for ![]() and
and ![]() for S). The corresponding resistance-pressure characteristics for the identified optimal configurations are presented in Figs. 5d and e. Even though we did not test all the possible 10
for S). The corresponding resistance-pressure characteristics for the identified optimal configurations are presented in Figs. 5d and e. Even though we did not test all the possible 10![]() 10 electrodes, the results represent optimal electrode design. The constructed deep learning ROMs can determine optimal design under different criteria and for other objectives at no additional simulation and training cost.
10 electrodes, the results represent optimal electrode design. The constructed deep learning ROMs can determine optimal design under different criteria and for other objectives at no additional simulation and training cost.
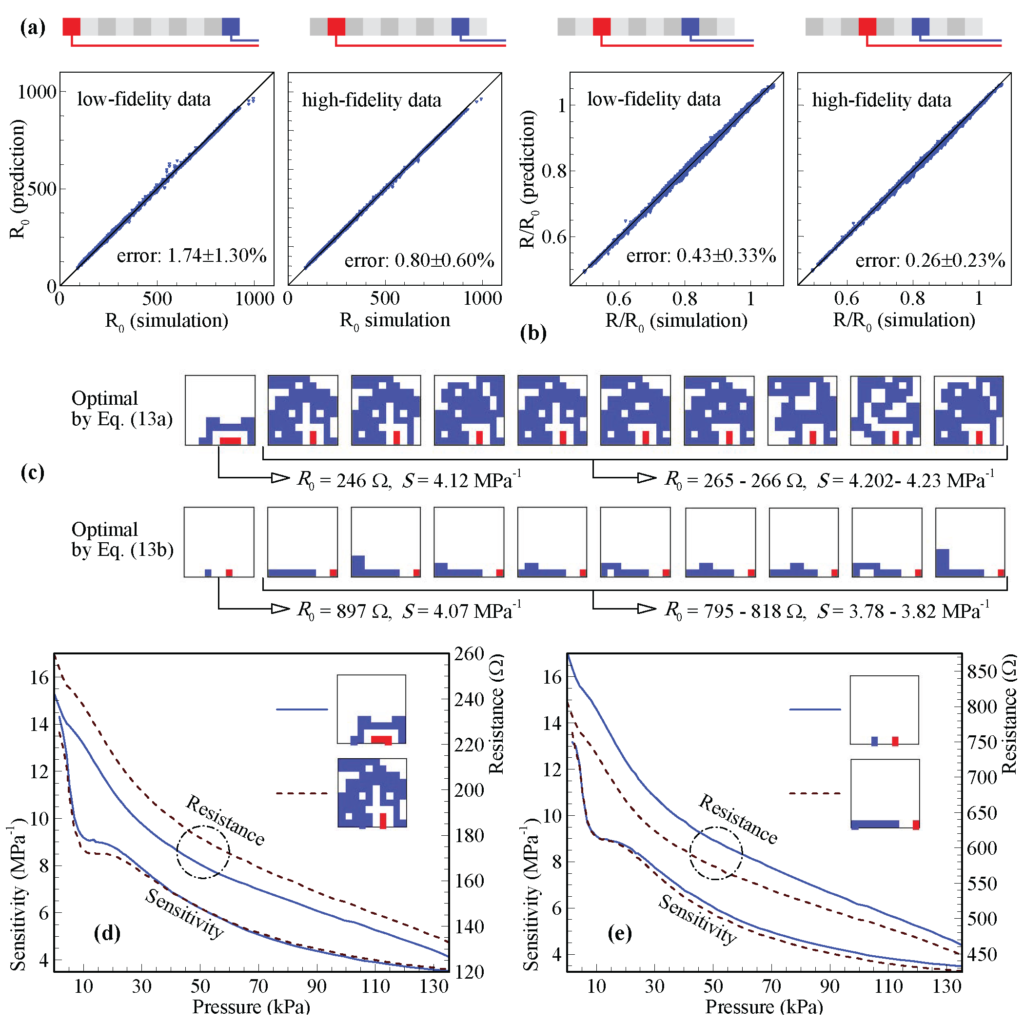
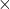 10 PCB matrices at 100 kPa. (a) Locations of various electrode connections used for the FEM simulations. (b) Scatter plots of predicted and FEM simulation results. (c) The optimal cases with high sensitivity and low power consumption (d), (e) The corresponding sensitivity- and resistance- pressure characteristics.
10 PCB matrices at 100 kPa. (a) Locations of various electrode connections used for the FEM simulations. (b) Scatter plots of predicted and FEM simulation results. (c) The optimal cases with high sensitivity and low power consumption (d), (e) The corresponding sensitivity- and resistance- pressure characteristics.Although we targeted the optimization for improved sensitivity and power consumption, the performance metamodels are versatile and provide cost-effective solutions to other optimization problems with different objective preferences. Moreover, transfer learning can be applied to refit the deep learning metamodels for other sensors more efficiently.
References
[1] X. Guan, Z. Wang, W. Zhao, H. Huang, S. Wang, Q. Zhang, D. Zhong, W. Lin, N. Ding, and Z. Peng, “Flexible Piezoresistive Sensors with Wide-Range Pressure Measurements Based on a Graded Nest-like Architecture,” ACS Applied Materials & Interfaces, vol. 12, no. 23, pp. 26137–26144, May 2020.
[2] R. Ramalingame, C. Gerlach, C. Muller, and O. Kanoun, “Influence of Electrode Design for Temperature and Pressure Sensing Behavior of Flexible and Bio-Compatible Nanocomposites,” 2016 Nanotechnology for Instrumentation and Measurement (NANOfIM), Sep. 2016.
[3] M. Abadi, P. Barham, J. Chen, Z. Chen, A. Davis, J. Dean, et al., “Tensorflow: A system for large-scale machine learning,” 12th USENIX Symposium on Operating Systems Design and Implementation, pp. 265–83, 2016.
[4] D. P. Kingma, and J. Ba, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980v9, Jan. 2017.
[5] M. Ashouri, and A. Hashemi, “A transfer learning metamodel using artificial neural networks applied to natural convection flows in enclosures,” arXiv preprint arXiv:2008.12483, Aug. 2020.
[6] R. C. Aydin, F. A. Braeu, and C. J. Cyron, “General multi-fidelity framework for training artificial neural networks with computational models,” Frontiers in Materials, vol. 6, Apr. 2019.