Conductive polymer composites exhibit electrical conductivity change when subjected to mechanical strain and are widely used in sensing applications. These composites are made of nonconductive polymers filled with dispersed conductive nanoparticles such as graphene, graphite, carbon nanotubes (CNTs), carbon black (CB), metallic nanoparticles, or hybrid fillers in which their equivalent electrical conductivity depends on percolation network and tunneling transport (i.e., the change in the conductive network and the average distance between the neighboring conductive fillers). A conductive polymer composite should contain a certain amount of conductive fillers (a critical value called percolation threshold where an insulator-conductor transition occurs) to achieve the highest sensitivity of the electrical conductivity to strain.
Flexible piezoresistive pressure/strain sensors are typically composed of a sensing layer made of a conductive polymer composite and a pair of electrodes. The sensor may be encapsulated with a polymer shell for integrity, biocompatibility, or waterproofing purposes. The higher the resistance sensitivity, these sensors can measure the applied pressure/strain more accurately. We present a simulation framework for predicting the mechanical and electrical responses of pressure and strain sensors made of conductive polymer piezoresistive composites. The numerical model uses the Finite Element Method to determine the three-dimensional deformation caused by an applied load and compute changes in the electric potential distribution induced by the change in resistivity and geometry of a sensing layer under deformation.
We first find the equivalent electrical resistance of the sensor at rest (before deformation). To do that, we solve the Laplace equation for the electrostatic potential distribution (∇²V=0) using the Finite Element Method (FEM). At the electrode connections, we either apply a constant current (Neumann boundary condition) or constant voltage (Dirichlet boundary condition) source as described by Eqs. (1) and (2), respectively. We apply the zero-electric-field boundary condition (∇V=0) elsewhere.
![]() (1)
(1)
![]() (2)
(2)
In Eq. (1), ![]() is the electric current flowing through the sensor,
is the electric current flowing through the sensor, ![]() is the electrical conductivity of the electrode material,
is the electrical conductivity of the electrode material, ![]() and
and ![]() are the surface areas of electrodes, and
are the surface areas of electrodes, and ![]() and
and ![]() are the vectors normal to them. In Eq. (2),
are the vectors normal to them. In Eq. (2), ![]() is the potential difference between the electrode connections.
is the potential difference between the electrode connections.
We use FEniCS [2,3] to solve the weak form of the Laplace equation given by
![]() (3)
(3)
where ![]() is the spatial domain,
is the spatial domain, ![]() is the boundary of
is the boundary of ![]() , and v is a test function. We compute the equivalent resistance as
, and v is a test function. We compute the equivalent resistance as ![]() . If a current source is applied at the electrode connections, we determine
. If a current source is applied at the electrode connections, we determine ![]() from the solution of electrostatic potential. We compute
from the solution of electrostatic potential. We compute ![]() for the case of a voltage source by integrating the current density (
for the case of a voltage source by integrating the current density (![]() ) over one of the electrode connections.
) over one of the electrode connections.
The equivalent resistance of a polymer composite sensor under loading is characterized by two primary factors: the classical change in the resistance due to change in geometry (change in the equivalent length and resistive area) and the change in the resistivity of the polymer composite under volume change (which affects the distance between conductive particles inside polymeric materials). To evaluate the first factor, we start by modeling the mechanical deformation before solving the Laplace equation for electric potential distribution on the deformed domain.
We ignore the viscoelastic response of polymers and simulate the sensors for quasi-static loadings. We consider compressible, nearly incompressible, and incompressible hyperelasticity. We implement the finite element variational form for the hyperelasticity problem using the total potential energy minimization approach in FEniCS (see [4] for details). We employ PETSc (Portable, Extensible Toolkit for Scientific Computation) [5] as the linear algebra backends to solve the linear systems of equations and use MUMPS (MUltifrontal Massively Parallel sparse direct Solver) [6] as a direct solver or GMRES (generalized minimal residual method) with AMG (algebraic multigrid) preconditioner as an iterative method if memory shortage is encountered.
Next, we use the known displacement function to move the mesh coordinates using an arbitrary Lagrangian-Eulerian (ALE) method in DOLFIN [7,8]. We find the equivalent electrical resistance by again solving the Laplace equation for the electrostatic potential distribution but on the deformed domain. To validate the implemented numerical code, we simulated a composite material under uniaxial loadings for which the exact analytical solutions are available (Fig. 1).

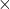 40
40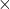 40 tetrahedral mesh and Lagrange P1 elements.
40 tetrahedral mesh and Lagrange P1 elements.To include the variation of the resistivity with volume, we apply semiempirical formulas based on percolation theory described by
![]() (4)
(4)
where ![]() and
and ![]() are the volume fraction of filler at the current composite state and the percolation threshold, and
are the volume fraction of filler at the current composite state and the percolation threshold, and ![]() and b are constants [9]. Given the geometrical change of the equivalent resistance, we find the unknown parameters using experimental resistance-pressure data. We attribute the composite volume change to the polymer matrix material (we assume that the volume change for filler nanoparticles is negligible). Therefore, the filler volume fraction at deformed state is given by
and b are constants [9]. Given the geometrical change of the equivalent resistance, we find the unknown parameters using experimental resistance-pressure data. We attribute the composite volume change to the polymer matrix material (we assume that the volume change for filler nanoparticles is negligible). Therefore, the filler volume fraction at deformed state is given by
![]() (5)
(5)
where ![]() is the filler volume fraction at rest state, and V and
is the filler volume fraction at rest state, and V and ![]() are the corresponding total volume of the composite polymer. We calculate the deformed volume of a composite using FEM results by
are the corresponding total volume of the composite polymer. We calculate the deformed volume of a composite using FEM results by
![]() (6)
(6)
where ![]() is the identity matrix and
is the identity matrix and ![]() is the displacement vector, or equivalently,
is the displacement vector, or equivalently,
![]() (7)
(7)
where ![]() is the third principal invariant of the right Cauchy-Green deformation tensor (defined by
is the third principal invariant of the right Cauchy-Green deformation tensor (defined by ![]() where
where ![]() is the deformation gradient).
is the deformation gradient).
We implemented our model on a piezoresistive pressure sensor recently presented by Guan et al. [1]. In their design, a bioinspired porous material (graded nest-like structure) is proposed for wide-range pressure measurement for regimes found in daily life – biosignals detection and robotic tactile sensing with high sensitivity and response time on top of good mechanical stability demonstrated through testing on a bicycle tire. Their prototype sensor had a 3-mm-thick sensing layer composed of porous TPU percolated with CB. The authors examined different CB/TPU mass ratios and porosities and reported that a 25 wt% CB/TPU and a porosity of about 74.2% (calculated value based on the reported mass ratio of NaCl as pore-forming agent) give the best piezoresistive performance. A flexible printed circuit board of polyimide (PI) film and metal electrodes with thicknesses of 150 ![]() m and 50
m and 50 ![]() m, respectively, were attached to one side of the sensing layer. The width and length of the tested device were both 10 mm.
m, respectively, were attached to one side of the sensing layer. The width and length of the tested device were both 10 mm.
To accurately describe the hyperelastic behavior and aging effect [10] of the polymer sensing layer, we developed a pseudo-linear elastic model in which we employed linear elasticity but with variable material properties. In foams subjected to large deformations, Poisson’s ratio and elastic moduli significantly change as the porosity changes [11,12]. Based on the analysis provided by Uhlířová and Pabst [12], the Poisson’s ratio (![]() ) of the TPU foam varies linearly with the porosity (
) of the TPU foam varies linearly with the porosity (![]() ):
):
![]() (8)
(8)
In Eq. (8), ![]() is the Poisson’s ratio for the TPU as the base material and
is the Poisson’s ratio for the TPU as the base material and ![]() is the Poisson’s ratio at the initial foam porosity of
is the Poisson’s ratio at the initial foam porosity of ![]() . Using the stress-strain curve reported in [1] and Eq. (8) for the Poisson’s ratio, we numerically predicted the modulus of elasticity for each data point. The porosity (
. Using the stress-strain curve reported in [1] and Eq. (8) for the Poisson’s ratio, we numerically predicted the modulus of elasticity for each data point. The porosity (![]() ) of foam at a deformed state with a volume of V is related to the undeformed state (at rest) by
) of foam at a deformed state with a volume of V is related to the undeformed state (at rest) by
![]() (9)
(9)
where ![]() and
and ![]() are the initial porosity and volume of the foam. Because the deformed volume and material properties are coupled, we implemented an iterative approach to find the material properties and the correct porosity for each data point. Starting from an initial guess for the Poisson’s ratio and modulus of elasticity, we performed FEM simulations and calculated the volume of the deformed foam using Eq. (7). We corrected the initial guesses until the results of porosity, modulus of elasticity, and Poisson’s ratio converged within 0.1%. The process diagram for fitting the stress-strain data using the proposed pseudo-linear elastic modeling is shown in Fig. 2 (left side). We conducted a mesh refinement study for the stringent case (largest deformation) before proceeding with a 64
are the initial porosity and volume of the foam. Because the deformed volume and material properties are coupled, we implemented an iterative approach to find the material properties and the correct porosity for each data point. Starting from an initial guess for the Poisson’s ratio and modulus of elasticity, we performed FEM simulations and calculated the volume of the deformed foam using Eq. (7). We corrected the initial guesses until the results of porosity, modulus of elasticity, and Poisson’s ratio converged within 0.1%. The process diagram for fitting the stress-strain data using the proposed pseudo-linear elastic modeling is shown in Fig. 2 (left side). We conducted a mesh refinement study for the stringent case (largest deformation) before proceeding with a 64![]() 64
64![]() 64 grid system (using Lagrange P1 elements) for the simulations. The mesh refinement analysis is presented in Fig. 2. The contours and the numbers within them are relative differences of the results of modulus of elasticity in percent compared to the selected mesh. As plotted in Fig. 2 (top right), we fitted the results of modulus of elasticity as
64 grid system (using Lagrange P1 elements) for the simulations. The mesh refinement analysis is presented in Fig. 2. The contours and the numbers within them are relative differences of the results of modulus of elasticity in percent compared to the selected mesh. As plotted in Fig. 2 (top right), we fitted the results of modulus of elasticity as
![]() (10)
(10)
in which the first expression accounts for the increased compressive modulus at low strains mainly attributed to the aging of the foam [10] and the second expression presents the major variation as normally described by a percolation model [13], however, we used a rational model to increase the fitting accuracy. In Eq. (10), ![]() is the modulus of elasticity for pure TPU,
is the modulus of elasticity for pure TPU, ![]() , and
, and ![]() . We note that Eq. (10) is valid for porosities in the range from 0.360 to 0.742 (in the range of available data). Using Eq. (10) for describing the variations of modulus of elasticity with porosity, we extracted the stress-strain curve through an iterative method as presented in Fig. 2 (bottom right).
. We note that Eq. (10) is valid for porosities in the range from 0.360 to 0.742 (in the range of available data). Using Eq. (10) for describing the variations of modulus of elasticity with porosity, we extracted the stress-strain curve through an iterative method as presented in Fig. 2 (bottom right).

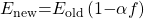 ,
,  is a relaxation factor and
is a relaxation factor and 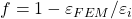 is the relative difference between the calculated and measured strain. We designed two loops to enhance convergence and stability. Top right: the variation of the modulus of elasticity with the porosity of the foam under compression. The contours present the results of the mesh refinement study. Bottom right: the stress-strain curve for the nanocomposite. The inner plots show the error decay associated with FEM iterations for each data point.
is the relative difference between the calculated and measured strain. We designed two loops to enhance convergence and stability. Top right: the variation of the modulus of elasticity with the porosity of the foam under compression. The contours present the results of the mesh refinement study. Bottom right: the stress-strain curve for the nanocomposite. The inner plots show the error decay associated with FEM iterations for each data point.The applied pressure affects both the microstructure and nanostructure of the nanocomposite foam and subsequently changes the resistivity of the sensing layer. Similar to the stress-strain curve, we derived the variations of the resistivity with porosity using the experimental resistivity-pressure characteristics reported in [1]. Using the data for an electrode configuration entitled “N3” in [1] (electrodes with three interdigitated lines), we found the variation of electrical conductivity (![]() ) as presented in Fig. 3 (top left) and fitted the data through the percolation theory as (
) as presented in Fig. 3 (top left) and fitted the data through the percolation theory as (![]() )
)
![]() (11a)
(11a)
or by substituting ![]() from Eq. (9),
from Eq. (9),
![]() (11b)
(11b)
where we obtained ![]() for the resistivity of the nanocomposite at rest. To improve the fitting accuracy for low strains, the coefficient
for the resistivity of the nanocomposite at rest. To improve the fitting accuracy for low strains, the coefficient ![]() is applied for
is applied for ![]() (i.e.,
(i.e., ![]() ), otherwise
), otherwise ![]() . As presented in Fig. 3, we performed a grid study on the stringent case (largest deformation) and found 64
. As presented in Fig. 3, we performed a grid study on the stringent case (largest deformation) and found 64![]() 60
60![]() 60 and 128
60 and 128![]() 120
120![]() 120 grids to be sufficient for mechanical and electrostatic simulations (using Lagrange P1 elements), respectively.
120 grids to be sufficient for mechanical and electrostatic simulations (using Lagrange P1 elements), respectively.
We used Eq. (11b) for taking into account the variation of nanocomposite electrical conductivity with porosity. Figure 3 (right side) presents the process diagram for the final model. The model takes in the pressure or strain and computes the equivalent resistance through an iterative approach. The resistance–pressure characteristics for the “electrode N3” as well as a new verification dataset (entitled “electrode N1” with one interdigitated line) are presented in Fig. 3 (bottom left). Animations of the mechanical deformation and electrostatic potential distributions are available in supplementary material S2.

 and R/R
and R/R are reported in comparison with 64
are reported in comparison with 64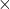 140
140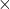 140 and 128
140 and 128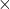 280
280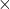 280 grids, respectively. Right side: the flowchart for the modeling approach. Bottom left: the resistance-pressure characteristics curve of the foam-based piezoresistive pressure sensor. We used separate experimental datasets from [1] for fitting and verifying the surrogate model for the variations of nanocomposite resistivity with porosity. The inner plot presents the contributions of each of the two factors (geometry and resistivity) to the equivalent resistance of the sensor at different compression strains. The product of the two factors gives the total resistance change.
280 grids, respectively. Right side: the flowchart for the modeling approach. Bottom left: the resistance-pressure characteristics curve of the foam-based piezoresistive pressure sensor. We used separate experimental datasets from [1] for fitting and verifying the surrogate model for the variations of nanocomposite resistivity with porosity. The inner plot presents the contributions of each of the two factors (geometry and resistivity) to the equivalent resistance of the sensor at different compression strains. The product of the two factors gives the total resistance change.As we see in the resistance-pressure characteristic curves in Fig. 3, the sensor performance is remarkably different for the two examined electrodes. At a fixed pressure/strain, the configuration of the electrodes negligibly affects the amount of volume change, and subsequently, the amount of change in the sensing layer resistivity (the black lines in the resistance-strain curve in Fig. 3, which are very close to each other). However, the change in the equivalent resistance due to geometry change is significantly impacted by electrode configuration (the red lines in the resistance-strain curve in Fig. 3). Especially for the N1 electrode, a compression loading decreases the effective surface area of the sensing layer between the electrodes (![]() where L and A are the lengths and cross-sectional areas scales), and therefore, adversely affects the equivalent resistance of the sensor. The reverse can also happen in a different electrode configuration (where a compression loading decreases the length scale). Thus, we sought to investigate the effect of electrode configuration on sensor performance. If available, the optimal topology has the highest sensitivity for the sensor at a specific range of working pressure (the sensitivity (S) is defined as the relative resistance change (
where L and A are the lengths and cross-sectional areas scales), and therefore, adversely affects the equivalent resistance of the sensor. The reverse can also happen in a different electrode configuration (where a compression loading decreases the length scale). Thus, we sought to investigate the effect of electrode configuration on sensor performance. If available, the optimal topology has the highest sensitivity for the sensor at a specific range of working pressure (the sensitivity (S) is defined as the relative resistance change (![]() ) per unit compression loading, i.e.,
) per unit compression loading, i.e., ![]() ). The outcome of the present model in optimizing the electrode topology for highest sensitivity and lowest power consumption is posted here.
). The outcome of the present model in optimizing the electrode topology for highest sensitivity and lowest power consumption is posted here.
References
[1] X. Guan, Z. Wang, W. Zhao, H. Huang, S. Wang, Q. Zhang, D. Zhong, W. Lin, N. Ding, and Z. Peng, “Flexible Piezoresistive Sensors with Wide-Range Pressure Measurements Based on a Graded Nest-like Architecture,” ACS Applied Materials & Interfaces, vol. 12, no. 23, pp. 26137–26144, May 2020.
[2] M. S. Alnaes, J. Blechta, J. Hake, A. Johansson, B. Kehlet, A. Logg, C. Richardson, J. Ring, M. E. Rognes, and G. N. Wells, “The FEniCS Project Version 1.5,” Archive of Numerical Software, vol. 3, no. 100, pages 9–23, Dec. 2015.
[3] H. P. Langtangen, “A FEniCS tutorial,” Lecture Notes in Computational Science and Engineering, vol. 84, pp. 1–73, 2012.
[4] K. B. Ølgaard and G. N. Wells, “Applications in solid mechanics,” Lecture Notes in Computational Science and Engineering, vol. 84, pp. 505–524, 2012.
[5] S. Abhyankar, J. Brown, E. M. Constantinescu, D. Ghosh, B. F. Smith, and H. Zhang, “PETSc/TS: A Modern Scalable ODE/DAE Solver Library,” arXiv:1806.01437, 2018.
[6] P. R. Amestoy, A. Buttari, J.-Y. L’Excellent, and T. Mary, “Performance and Scalability of the Block Low-Rank Multifrontal Factorization on Multicore Architectures,” ACM Transactions on Mathematical Software, vol. 45, no. 1, pp. 1–26, Mar. 2019.
[7] A. Logg and G. N. Wells. DOLFIN: Automated finite element computing. ACM Transactions on Mathematical Software, vol. 32, no. 20, pp. 1–28, Apr. 2010.
[8] A. Logg, G. N. Wells, and J. Hake, “DOLFIN: a C++/Python finite element library,” Lecture Notes in Computational Science and Engineering, vol. 84, pp. 173–225, 2012.
[9] W. Bauhofer and J. Z. Kovacs, “A review and analysis of electrical percolation in carbon nanotube polymer composites,” Composites Science and Technology, vol. 69, no. 10, pp. 1486–1498, Aug. 2009.
[10] A. Tcharkhtchi, S. Farzaneh, S. Abdallah-Elhirtsi, B. Esmaeillou, F. Nony, and A. Baron, “Thermal Aging Effect on Mechanical Properties of Polyurethane,” International Journal of Polymer Analysis and Characterization, vol. 19, no. 7, pp. 571–584, Oct. 2014.
[11] B. Sanborn and B. Song, “Poisson’s ratio of a hyperelastic foam under quasi-static and dynamic loading,” International Journal of Impact Engineering, vol. 123, pp. 48–55, Jan. 2019.
[12] T. Uhlířová and W. Pabst, “Poisson’s ratio of porous and cellular materials with randomly distributed isometric pores or cells,” Journal of the American Ceramic Society, vol. 103, no. 12, pp. 6961–6977, May 2020.
[13] J. Kováčik, “Correlation between Young’s modulus and porosity in porous materials,” Journal of Materials Science Letters, vol. 18, no. 13, pp. 1007–1010, 1999.